Mesh Processing

Atomic Operations

The core of the mesh processing pipeline relies on three atomic mesh operations: edge split, edge flip, and edge collapse. Each of these modifies the mesh’s connectivity in a small, localized way, enabling higher-level algorithms like subdivision, remeshing, and simplification.

• Edge collapse: Removes an edge and merges its two vertices, reducing polygon count for simplification while preserving overall shape as much as possible.
• Edge split: Divides an edge into two by inserting a new vertex at a specified position (usually the midpoint). This is used to increase mesh resolution or refine specific regions.
• Edge flip: Changes the diagonal of the quadrilateral formed by two adjacent triangles, improving triangle quality or redistributing edge directions for a more uniform mesh.

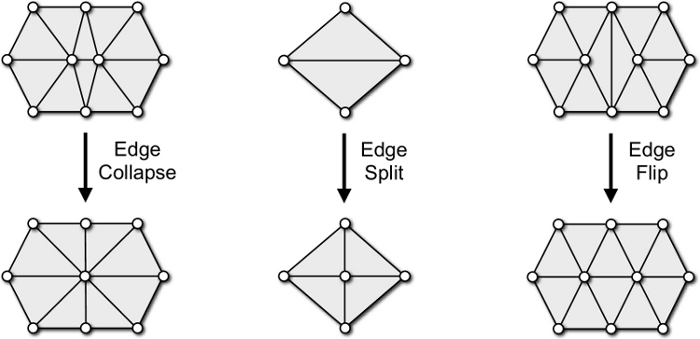
These operations are performed in constant time thanks to the half-edge data structure, which stores explicit adjacency information between vertices, edges, and faces. With pointers to a half-edge’s origin vertex, twin, and next edges, updates can be made locally without scanning the entire mesh.

To ensure mesh integrity after any operation, a validate function is called. This function checks for common issues such as:

• Broken twin relationships
• Inconsistent face loops
• Degenerate faces (zero area)
• Duplicate or dangling vertices

By combining efficient local operations with immediate validation, the system maintains a robust, well-formed mesh throughout processing, even during large sequences of transformations.

Subdivision

Loop subdivision is a surface refinement algorithm designed for triangle meshes. It takes an existing mesh and generates a smoother, higher-resolution version by repeatedly splitting edges and repositioning vertices according to carefully chosen weights.

In each iteration, every triangle is split into four smaller triangles. This can be done by splitting every edge of the mesh in any order, any flipping new edges that touch a new and old vertex. Then, existing vertices are moved to new positions that smooth the surface while preserving the original shape. The new position is calculated from averaging the positions of the vertex’s one-ring neighbors.

Simplification

Quadric Error Simplification is a widely used algorithm for reducing the number of polygons in a mesh while preserving its overall shape as much as possible. It works by repeatedly collapsing edges in an order that minimizes geometric error.

For every face, we define a quadric, a 4×4 symmetric matrix that encodes the squared distance to the plane of the face. For every vertex, we define its quadric as the sum of the quadrics of its neighboring faces. For every edge, we define its quadric as the sum of quadrics of the two vertices it touches. 

Distance of a point to a plane can be calculated as the product of the position, the plane’s quadric, and the position’s transpose. Extending this to the quadric of an edge, this matrix multiplication is a compact way to sum the squared distances from the point to all the edge’s neighboring planes. A small error value means the vertex is close to all its neighboring planes, where collapsing it will have little impact on the surface shape, while a large error value means the vertex is far from one or more of those planes, collapsing it risks distorting the mesh significantly.

Thus, the point on an edge that minimizes the error value is the optimal position of the vertex that a particular edge collapses to. Therefore, we can minimize geometric error by repeatedly collapsing edges with the minimum error value. To do this, the quadric of every edge is precomputed, and every edge is added to a heap based on its minimum error value. The simplification process then proceeds as follows:

• While the target face or vertex count hasn’t been reached, extract the edge with the smallest error from the heap.
• Collapse the edge to its optimal position.
• Update the quadrics for the affected vertex and its neighbors.
• Recompute the error values for edges connected to the updated vertex.
• Update their positions in the heap.

This greedy approach ensures that each step makes the smallest possible “damage” to the surface, and because the quadric error metric accumulates plane distances, the algorithm naturally preserves important features like sharp edges and corners longer than flat or low-detail areas.

Denoising

Bilateral mesh denoising is a smoothing technique that removes small surface noise from a mesh without blurring important features like sharp edges and corners. It works by adapting the bilateral filter to operate on 3D geometry.

Instead of averaging each vertex with all of its neighbors equally, the bilateral filter considers two things:

• How similar the surface orientation is: vertices on the same smooth surface contribute more than those across a sharp edge.
• How close the neighbor is in space: nearby vertices have more influence.

Once the filter computes a target smoothed position for a vertex, the vertex is moved only along its surface normal. This prevents the surface from shrinking or distorting while still removing unwanted noise. By combining these factors, the algorithm selectively smooths flat or gently curved regions while leaving edges crisp.